递归与归并排序

在本文中，我们将简单讨论递归的原理以及使用场景、 Java 中的递归以及归并排序（Merge Sort）。

递归

递归在计算机科学中是一种非常常见的，同于解决某些特定问题的方法。递归可以用于解决一些可以被分解为规模更小的相同问题的问题。递归的基本原理是将问题分解为规模更小的相同问题，直到问题的规模变得足够小，可以直接解决。

递归的基本原理可以用下面的代码表示：

void recursiveMethod() {
    // ...
    recursiveMethod(); // 递归调用，一个方法调用自己
    // ...
}

void someMethod() {
    recursiveMethod(); // 调用递归方法
}

当然，递归也有一些缺点，比如递归调用会占用更多的内存，因为每次递归调用都会在内存中创建一个新的方法调用栈。

同时，你应该发现了，如果直接运行上面的代码，递归方法对自己的调用将会无限继续下去，因此我们需要在递归方法中添加一个终止条件，以避免无限递归。

递归的应用与其 Java 实现

求和

我们直接使用示例来说明递归的使用，假设我们要计算以下函数的值：

$$
f(n) = \sum_{i=1}^{n} i = 1 + 2 + 3 + \cdots + n
$$

那么其实我们可以发现，递归可以用来解决这个问题，因为 $\sum_{i=1}^{n}$ 的结果可以被分解为 $n + \sum_{i=1}^{n-1}$，而 $\sum_{i=1}^{n-1}$ 又可以被分解为 $n-1 + \sum_{i=1}^{n-2}$，以此类推，直到 $n=1$ 时，$\sum_{i=1}^{1} = 1$，同时我们可以发现，这个问题的终止条件就是 $n=1$，因为此时我们不需要再继续递归计算了（而是直接返回 1）。

下面是 Java 中的代码实现：

/**
 * 计算 1 + 2 + 3 + ... + n 的和
 * @param n 非负整数
 * @return 1 + 2 + 3 + ... + n 的和
 */
private static int sum(int n) {
    if (n == 1) { // 如果 n 是 0，说明算到和的最后一步了，直接返回 1（递归的终止条件）
        return 1;
    } else {
        return n + sum(n - 1); // 否则，返回 n 加上 1 + 2 + 3 + ... + (n - 1) 的和，这样就可以递归地计算 1 + 2 + 3 + ... + n 的和
    }
}

这就是一个最基础的递归示例。

阶乘

我们再来看一个递归的经典问题，计算阶乘：

$$
f(n) = n! = n \times (n-1) \times (n-2) \times \cdots \times 1
$$

阶乘也可以被分解成一个更小的相同问题，即 $n! = n \times (n-1)!$。因此，我们可以使用递归来解决这个问题。

需要考虑到的是，阶乘的终止条件是 $n=1$，此时 $1! = 1$。

下面是 Java 中的代码实现：

/**
 * 计算 n 的阶乘
 * @param n 非负整数
 * @return n 的阶乘
 */
private static int factorial(int n) {
    if (n == 1) { // 如果 n 是 1，说明算到阶乘的最后一步了，直接返回 1（递归的终止条件）
        return 1;
    } else {
        return n * factorial(n - 1); // 否则，返回 n 乘以 n - 1 的阶乘，这样就可以递归地计算 n 的阶乘
    }
}

指数

如果我们要计算指数，那么我们可以将其定义为：

$$
f(x, n) = x^n = x \times x^{n-1} = x \times f(x, n-1) \text{, where } n \in \mathbb{N}_0
$$

这个问题的终止条件是 $n=0$，此时 $x^0 = 1$。

下面是 Java 中的代码实现：

/**
 * 计算 x 的 n 次方
 * @param x 非负整数（我们不考虑负数/小数的情况，虽然其实是可以的）
 * @param n 非负整数
 * @return x 的 n 次方
 */
private static double power(int x, int n) {
    if (n == 0) { // 如果 n 是 0，说明算到指数的最后一步了，直接返回 1（递归的终止条件）
        return 1;
    } else {
        return x * power(x, n - 1); // 否则，返回 x 乘以 x 的 n - 1 次方，这样就可以递归地计算 x 的 n 次方
    }
}

负数指数

上面的问题中，我们假设了 $n$ 是非负整数，那么如果 $n$ 是负数呢？我们都知道：

$$
x^{-n} = \frac{1}{x^n}
$$

那么其实，只要我们正常计算 $x^{|n|}$，然后返回其倒数即可。或者，我们可以使用下面的定义：

$$
f(x, n) = \begin{cases}
1, & \text{if } n = 0 \newline
x \times f(x, n-1), & \text{if } n > 0 \newline
\frac{1}{x \times f(x, |n| - 1)}, & \text{if } n < 0
\end{cases}
\text{where } n \in \mathbb{Z}
$$

在这种情况下，如果 $n$ 是正数，我们就按照正常的递归计算 $x^n$。但是，如果 $n$ 是负数，我们就计算 $x$ 乘以 $x$ 的 $|n|-1$ 次方的倒数。注意到了吗？这里使用了 $|n|$ 来表示 $n$ 的绝对值，这样递归计算完后，我们将其与 $x$ 相乘，我们就得到了 $x^{|n|}$，然后计算其倒数即可。

下面是 Java 中的代码实现：

/**
 * 计算 x 的 n 次方
 * @param x 非负整数（我们不考虑负数/小数的情况，虽然其实是可以的）
 * @param n 整数
 * @return x 的 n 次方
 */
private static double power(int x, int n) {
    if (n == 0) { // 如果 n 是 0，说明算到指数的最后一步了，直接返回 1（递归的终止条件）
        return 1;
    } else {
        if (n > 0) { // 如果 n 是正数
            return x * power(x, n - 1); // 返回 x 乘以 x 的 n - 1 次方
        } else { // 如果 n 是负数
            return 1 / (x * power(x, Math.abs(n) - 1)); // 返回 1 除以 x 乘以 x 的 |n| - 1 次方，注意到了吗，此后所有的递归调用中指数 n 都是正数了
        }
    }
}

斐波那契数列

斐波那契数列是另一个经典的递归问题，其定义如下：

$$
f(n) = \begin{cases}
0, & \text{if } n = 0 \newline
1, & \text{if } n = 1 \newline
f(n-1) + f(n-2), & \text{if } n > 1
\end{cases}
\text{where } n \in \mathbb{N}_0
$$

也就是说，在这个数列中，第一项是 0，第二项是 1，之后的每一项都是前两项的和。

这个问题的递归方法已经非常明显了，因为上面的定义直接使用了 $f(n) = f(n-1) + f(n-2)$，因此我们可以直接使用递归来解决这个问题。

这个问题的终止条件是 $n=0$ 或 $n=1$，此时 $f(0) = 0$，$f(1) = 1$。

下面是 Java 中的代码实现：

/**
 * 计算斐波那契数列的第 n 项
 * @param n 非负整数
 * @return 斐波那契数列的第 n 项
 */
private static int fibonacci(int n) {
    if (n == 0) { // 如果 n 是 0，直接返回 0（递归的终止条件）
        return 0;
    } else if (n == 1) { // 如果 n 是 1，直接返回 1（递归的终止条件）
        return 1;
    } else {
        return fibonacci(n - 1) + fibonacci(n - 2); // 否则，返回 f(n-1) + f(n-2)，这样就可以递归地计算斐波那契数列的第 n 项
    }
}

判断质数

偶尔，递归也可以代替循环使用。

判断一个数是否是质数。首先，质数是大于 1 的自然数，且只能被 1 和自身整除。我们可以使用循环来解决这个问题：

/**
 * 判断一个数是否是质数
 * @param n 非负整数
 * @return 如果 n 是质数，返回 true；否则，返回 false
 */
private static boolean isPrime(int n) {
    if (n <= 1) { // 如果 n 是 0 或 1，直接返回 false
        return false;
    }
    for (int i = 2; i < n; i++) { // 从 2 到 n-1 遍历
        if (n % i == 0) { // 如果 n 能被 i 整除，说明 n 不是质数
            return false;
        }
    }
    return true; // 如果 n 不能被 2 到 n-1 之间的任何数整除，说明 n 是质数
}

但是，其实我们可以使用递归来解决这个问题。我们可以将上面的循环转换为递归：

/**
 * 判断一个数是否是质数
 * @param n 非负整数
 * @param i 从 2 开始的整数
 * @return 如果 n 是质数，返回 true；否则，返回 false
 */
private static boolean isPrime(int n, int i) {
    if (n <= 1) { // 如果 n 是 0 或 1，直接返回 false
        return false;
    }
    if (i == n) { // 如果 i 等于 n，说明 n 不能被 2 到 n-1 之间的任何数整除，说明 n 是质数
        return true;
    }
    if (n % i == 0) { // 如果 n 能被 i 整除，同时 i 不等于 n（因为如果等于的话，上面的 if 语句就会返回 true），说明 n 不是质数
        return false;
    }
    return isPrime(n, i + 1); // 否则，如果两个情况都没有达到，我们就仍然不能确定，继续递归调用判断 n 能否被 i+1 整除
}

这样，我们就使用递归来判断一个数是否是质数了。

进制转换

递归还可以用于进制转换。我们知道，将一个十进制数转换为其他进制数，可以使用以下方法：

将十进制数除以目标进制数，得到商和余数；
余数即为目标进制数中的倒数第一位；
将商继续除以目标进制数，得到新的商和余数；
此时的新余数即为目标进制数中的倒数第二位；
将新的商继续除以目标进制数，得到新的商和余数；
以此类推，直到商为 0。

这个问题可以使用递归来解决，因为每一步都是相同的除法运算。这个问题的终止条件是商为 0，此时我们就可以直接返回。

下面是 Java 中的代码实现：

/**
 * 将一个十进制数转换为目标进制数
 * @param n 十进制数
 * @param base 目标进制数
 * @param result 目前的结果
 * @return 十进制数 n 转换为目标进制数的结果
 */
private static String toBase(int n, int base, String result) {
    if (n == 0) { // 如果 n 是 0，直接返回结果
        return result;
    } else {
        int remainder = n % base; // 余数
        // 将余数转换为字符，这里适用于类似于十六进制的情况，如果余数小于 10，直接转换为字符 '0' 到 '9'，否则转换为字符 'A' 到 'F'
        // 这个转换方法如果使用十进制及以下的进制数，就可以去掉
        char digit = (char) (remainder < 10 ? remainder + '0' : remainder - 10 + 'A');
        // 转换的另外一个使用 if 的写法为
        if (remainder < 10) {
            digit = (char) (remainder + '0'); // 这样，基于 ASCII 码，我们就可以获得 '0' 到 '9' 的字符
        } else {
            digit = (char) (remainder - 10 + 'A'); // 这样，基于 ASCII 码，我们就可以获得 'A' 到 'F' 的字符，要注意的是，我们需要减去 10，这样我们就可以将 'A' 作为起始字符
        }
        return convert(n / base, base, digit + result); // 递归调用，继续转换，其中调用的参数分别为：计算的商、目标进制数、当前结果（用于继续向前添加）
    }
}

这样，我们就可以使用递归来将一个十进制数转换为目标进制数了。

归并排序

合并两个有序数组

在讨论归并排序之前，我们先来看一个简单的问题：合并两个有序数组。这个部分将对归并排序的理解有所帮助。

假设我们有两个有序数组 a 和 b，我们要将这两个数组合并为一个有序数组 c。我们可以使用下面的方法：

从数组 a 和 b 的第一个元素开始，比较两个元素的大小；
将较小的元素放入数组 c；
将较小元素所在的数组的索引向后移动一位；
重复上面的步骤，直到其中一个数组的所有元素都被放入数组 c；
将另一个数组的剩余元素放入数组 c。

如果将这个步骤可视化，我们可以得到：

我们有两个要排序的数组 a 和 b，以及一个空数组 c。同时，我们有两个指针 i 和 j 分别存储数组 a 和 b 的当前索引；以及一个指针 k 存储数组 c 的当前索引；
1
2
3
4
5
6
a = [1, 3, 5, 7, 9]
b = [2, 4, 6, 8, 10]
c = []
i = 0
j = 0
k = 0
那么，我们可以比较 a[i] 和 b[j] 的大小，他们分别是 1 和 2，1 更小，因此我们将 1 放入数组 c，同时 i 和 k 向后移动一位：
1
2
3
4
5
6
a = [1, 3, 5, 7, 9]
b = [2, 4, 6, 8, 10]
c = [1]
i = 1
j = 0
k = 1
这样，实际上数组 a 的第一个元素就不会再被考虑了。同时我们知道下一次向数组 c 添加的是第二个元素。
重复上面的步骤，继续比较 a[i] 和 b[j] 的大小，他们分别是 3 和 2，2 更小，因此我们将 2 放入数组 c，同时 j 和 k 向后移动一位：
1
2
3
4
5
6
a = [1, 3, 5, 7, 9]
b = [2, 4, 6, 8, 10]
c = [1, 2]
i = 1
j = 1
k = 2
我们需要重复上面的步骤，直到其中一个数组的所有元素都被放入数组 c。这时我们也可以确定，另外一个数组的所有元素都比数组 c 中目前存在的元素大，因此我们可以直接将另外一个数组的所有剩余元素放入数组 c。

Java 实现

下面是 Java 中的合并两个有序数组的代码实现：

/**
 * 合并两个有序数组
 * @param list1 第一个有序数组
 * @param list2 第二个有序数组
 * @return 合并后的有序数组
 */
private static ArrayList<Integer> merge(ArrayList<Integer> list1, ArrayList<Integer> list2) {
    ArrayList<Integer> merged = new ArrayList<>(); // 合并后的数组
    int i = 0, j = 0; // 两个数组的索引
    while (i < list1.size() && j < list2.size()) { // 两个数组都还有元素
        if (list1.get(i) <= list2.get(j)) { // 如果第一个数组的元素更小（或相等）
            merged.add(list1.get(i)); // 将第一个数组的元素加入合并后的数组
            i++; // 第一个数组的索引加一
        } else { // 否则（第二个数组的元素更小）
            merged.add(list2.get(j)); // 将第二个数组的元素加入合并后的数组
            j++; // 第二个数组的索引加一
        }
    }
    while (i < list1.size()) { // （只有）第一个数组还有元素
        merged.add(list1.get(i)); // 将第一个数组的元素加入合并后的数组
        i++; // 第一个数组的索引加一
    }
    while (j < list2.size()) { // （只有）第二个数组还有元素
        merged.add(list2.get(j)); // 将第二个数组的元素加入合并后的数组
        j++; // 第二个数组的索引加一
    }
    return merged; // 返回合并后的数组
}

注意，由于我们使用了 ArrayList 来存储合并后的数组，因此我们可以直接使用 add 方法来添加元素，而且不需要使用 k 来记录合并后的数组的索引。

归并排序原理

接下来我们就可以讲解归并排序了。

归并排序的基本原理为，讲一个数组从中间分为两部分，然后分别将这两部分从中间继续分解，直到每个部分只有一个元素。然后，我们使用合并两个有序数组的方法，将这些部分合并为一个有序数组。

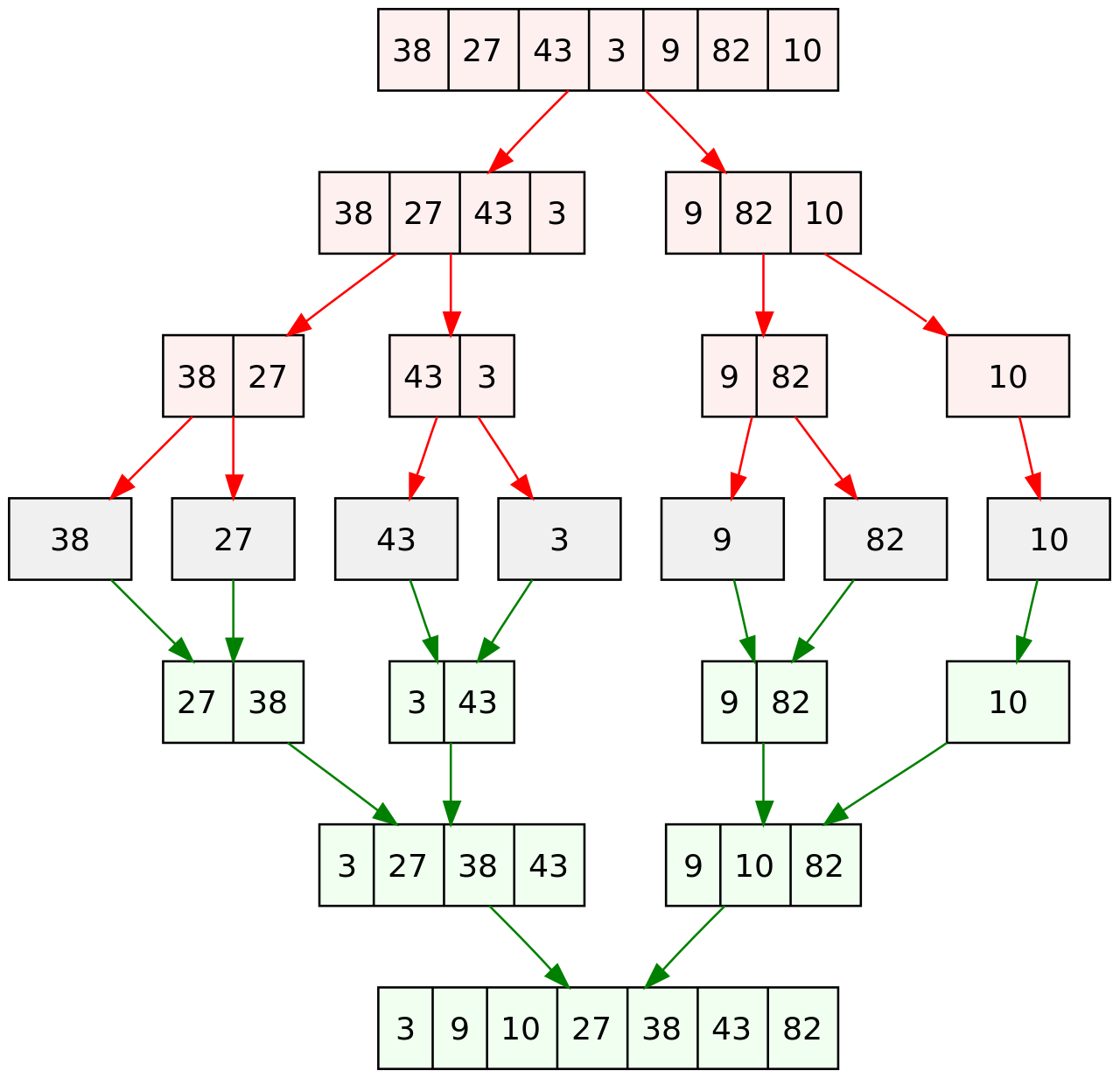
归并排序示意图

在上图中，红色的部分表示分割数组的过程，绿色的部分表示合并数组的过程。

我们会发现，首先我们将数组 [38, 27, 43, 3, 9, 82, 10] 分割。由于数组的长度为 7，分割线为 7 / 2 = 3，因此我们将数组分割为 [38, 27, 43, 3] 和 [9, 82, 10]。然后，由于这两个数组的长度都大于 1，我们继续分割，分别分割为 [38, 27]、[43, 3]、[9, 82] 和 [10]。然后，我们继续分割，直到每个部分只有一个元素。

由于我们可以认为每个部分只有一个元素的数组永远是有序的，我们就可以直接使用合并两个有序数组的方法，将这些部分重新合并为一个有序数组了。

归并排序 Java 实现

下面是 Java 中的归并排序的代码实现：

public class MergeSort {
    /**
     * 将一个数组中的两个有序序列合并成一个新的有序序列
     * @param list 要排序的数组
     * @param left 数组的左边界
     * @param middle 数组的中间元素的下标
     * @param right 数组的右边界
     */
    private static void merge(ArrayList<Integer> list, int left, int middle, int right) {
        int n1 = middle - left + 1; // 左半部分的元素个数
        int n2 = right - middle; // 右半部分的元素个数

        ArrayList<Integer> leftList = new ArrayList<>(); // 存储左半部分的元素
        ArrayList<Integer> rightList = new ArrayList<>(); // 存储右半部分的元素

        for (int i = 0; i < n1; i++) { // 将左半部分的元素复制到 leftList
            leftList.add(list.get(left + i));
        }

        for (int i = 0; i < n2; i++) { // 将右半部分的元素复制到 rightList
            rightList.add(list.get(middle + 1 + i));
        }

        int i = 0, j = 0; // i 是 leftList 的下标，j 是 rightList 的下标，分别用于遍历左右两部分来进行合并
        int k = left; // k 是 list 的下标，用来指定合并中的元素应该放在 list 的哪个位置

        while (i < n1 && j < n2) { // 只要左右两部分都还有元素，就继续合并
            if (leftList.get(i) <= rightList.get(j)) { // 如果左边元素数组中的元素更小（或相等）
                list.set(k, leftList.get(i)); // 将左边元素数组中的元素放入 list
                i++; // 左边元素数组的下标加一，不再考虑这个已经被放入 list 的元素
            } else { // 否则（右边元素数组中的元素更小）
                list.set(k, rightList.get(j)); // 将右边元素数组中的元素放入 list
                j++; // 右边元素数组的下标加一，不再考虑这个已经被放入 list 的元素
            }
            k++; // list 的下标加一，开始向下一个位置放入元素
        }

        while (i < n1) { // 如果只有左边元素数组还有元素
            list.set(k, leftList.get(i)); // 将左边元素数组中的元素放入 list
            i++; // 左边元素数组的下标加一，不再考虑这个已经被放入 list 的元素
            k++; // list 的下标加一，开始向下一个位置放入元素
        }

        while (j < n2) { // 如果只有右边元素数组还有元素
            list.set(k, rightList.get(j)); // 将右边元素数组中的元素放入 list
            j++; // 右边元素数组的下标加一，不再考虑这个已经被放入 list 的元素
            k++; // list 的下标加一，开始向下一个位置放入元素
        }

        // 合并完成，此时 list 中从左边界（left）到右边界（right）的元素都已经是有序的了
    }

    /**
     * 合并排序
     * @param list 要排序的数组
     * @param left 数组的左边界
     * @param right 数组的右边界
     */
    private static void mergeSort(ArrayList<Integer> list, int left, int right) {
        if (left < right) { // 如果左边界小于右边界，说明数组至少有两个元素，可以继续分割
            int middle = (left + right) / 2; // 找到中间元素的下标
            mergeSort(list, left, middle); // 对左半部分排序
            mergeSort(list, middle + 1, right); // 对右半部分排序
            merge(list, left, middle, right); // 合并左右两部分
        }
    }

    public static void main(String[] args) {
        ArrayList<Integer> list = new ArrayList<>();
        list.add(-10);
        list.add(54);
        list.add(-18);
        list.add(-32);
        list.add(32);
        list.add(384);
        list.add(44);
        list.add(44);
        list.add(16);
        list.add(1);
        list.add(5);
        list.add(80);
        list.add(-32);
        list.add(0);
        list.add(48);
        list.add(384);

        System.out.println("Before sorting: ");
        System.out.println(list);

        // 调用合并排序方法
        // 最开始的左边界是数组的第一个元素，下标为0
        // 最开始的右边界是数组的最后一个元素，下标为数组长度-1
        mergeSort(list, 0, list.size() - 1);

        System.out.println("After sorting: ");
        System.out.println(list);
    }
}

要注意的是，我们就算在合并时也一直在操作同一个数组。只不过我们使用了 left、middle 和 right 来指定数组的左右边界。

我们要合并的数组中，第一个数组一定是从 left 到 middle 的元素，第二个数组一定是从 middle + 1 到 right 的元素。而我们可以将这些元素复制出来存储一下，然后直接在原数组中进行合并，因为我们知道合并后的元素一定会被置于原数组的 left 到 right 的区间。

这里我们同样使用了递归的概念，因为我们会发现，每次将数组分割为两部分后，实际上就是对单独的部分进行归并排序。这个分割的过程的终止条件是每个部分只有一个元素，然后我们就可以开始进行合并，反向的将递归走完回到初始点。

GL & HF!

本文采用署名-非商业性使用-相同方式共享 4.0 国际许可协议，转载请注明出处。