在本文中,我们将简单了解大 $O$ 表示法。
什么是大 $O$ 表示法?
大 $O$ 表示法是一种用于描述算法的效率的标准符号。它描述的是算法的时间复杂度(Time Complexity),即算法执行所需的时间,以及这个时间如何随着输入规模的增加而变化。大 $O$ 表示法可以表示算法的最优、平均和最差情况下的时间复杂度。
大部分情况下,我们关注的是算法时间复杂度函数的上界,即最坏情况下的时间复杂度。这是因为在实际应用中,我们通常更关心算法在最坏情况下的性能表现。
$O$ 这个字母原本的定义为“Order of”(阶数),使用拉丁语中的大写字母 $Omicron$ 表示,但由于字型相同,也可以理解为拉丁字母大写 “O”.
由于运行代码的计算机的性能不同,所以我们通常不关心具体的运行时间(毫秒、秒等),而是关心算法的时间复杂度(同样的时间复杂度在同样的计算机上需要的运行时间一样),大 $O$ 表示法的参数即为时间复杂度,以及其如何随着输入规模 $n$ 的增加而变化。你通常也可以认为其表示一个循环内部的代码执行多少次才可以完成算法的执行。
恒定时间复杂度 $O(1)$
恒定时间复杂度 $O(1)$ 表示操作的执行时间与输入规模 $n$ 无关,即算法的执行时间是一个常数。这种算法的执行时间是固定的,不随着输入规模的增加而变化。这类操作通常包含:
- 数学运算(加减乘除、取模等)
- 直接访问数组元素
- 存取变量
- 逻辑判断(if-else、switch-case 等)
- 函数返回参数
下述是一个恒定时间复杂度 $O(1)$ 的示例:
1 | public class ConstantTimeComplexity { |
上述代码中,我们执行了一系列的操作,包括数学运算、数组元素访问、变量存取等,这些操作的执行时间是固定的,不随着输入规模的增加而变化,因此其时间复杂度是 $O(1)$。
注意!就算数组有不同的长度,访问数组元素的时间复杂度仍然是 $O(1)$,因为数组的访问是通过索引来实现的,不需要遍历整个数组。
线性时间复杂度 $O(n)$
线性时间复杂度 $O(n)$ 表示操作的执行时间与输入规模 $n$ 成正比,即算法的执行时间随着输入规模的增加而线性增长。这类操作通常包含:
- 遍历数组、链表、树等数据结构
- 递归操作
- 线性搜索、线性查找等
在现实生活中,我们可以使用以下场景理解:如果你需要读一本书,而你每读一页都需要花费一分钟,那么读完整本书所需的时间就是书的页数(单位分钟)。这就是一个线性时间复杂度 $O(n)$ 的例子。
下述是一个线性时间复杂度 $O(n)$ 的示例:
1 | public class LinearTimeComplexity { |
上述代码中,我们遍历了一个长度为 $10$ 的数组,如果将数组的长度定义为 $n$,因此遍历数组的时间复杂度是 $O(n)$。同时,你应该注意到,System.out.println 方法同样运行了一共 $n$ 次。
要注意的是,线性时间复杂度 $O(n)$ 并不意味着算法的执行时间是固定的,而是随着输入规模的增加而线性增长。
另外,由于 System.out.println 方法以及其中的,获取数组元素的操作都是 $O(1)$ 的,因此整个代码的时间复杂度是 $O(n)$。
如果考虑以下线性搜索的例子:
1 | public class LinearSearch { |
其时间复杂度仍然是 $O(n)$,因为就算有可能要寻找的元素在数组中间就被找到了,但是在最坏情况下,要寻找的元素在数组的最后一个位置,这时候就需要遍历整个数组。
二次时间复杂度 $O(n^2)$
二次时间复杂度 $O(n^2)$ 表示操作的执行时间与输入规模 $n$ 的平方成正比,即算法的执行时间随着输入规模的增加而平方增长。这类操作通常包含:
- 嵌套循环
- 一些排序算法(如冒泡排序、选择排序等)
下述是一个二次时间复杂度 $O(n^2)$ 的示例:
1 | public class QuadraticTimeComplexity { |
上述代码中,我们使用了两个嵌套循环,其中外层循环的执行次数是 $n$,内层循环的执行次数也是 $n$,因此整个代码的时间复杂度是 $O(n^2)$。
如果考虑以下例子:
1 | public class Main { |
其时间复杂度则成为了 $O(n^3)$,因为每层循环的执行次数都是 $n$。接下来不再赘述,你可以自行推导出 $O(n^4)$、$O(n^5)$ 等的时间复杂度。
对数时间复杂度 $O(\log n)$
对数时间复杂度 $O(\log n)$ 表示操作的执行时间与输入规模 $n$ 的对数成正比(此处的对数函数以 $2$ 为底)。二分查找(Binary Search)是一个典型的对数时间复杂度的例子。
下述是一个对数时间复杂度 $O(\log n)$ 的示例:
1 | public class BinarySearch { |
上述代码中,我们使用了一个循环,每次将 $i$ 乘以 $2$,直到 $i$ 大于 $n$,这个循环的执行次数是 $O(\log n)$,因为每次循环 $i$ 的值都会翻倍并以指数级增长来逼近 $n$。你可以通过运行代码来验证。如果 $n = 2000$,那么循环的执行次数是 $11$,符合计算 $log_2(2000) \approx 11.2877$。
同样的,二分查找的时间复杂度是 $O(\log n)$,因为每次查找都会将查找范围缩小一半。
线性对数时间复杂度 $O(n \log n)$
线性对数时间复杂度 $O(n \log n)$ 表示操作的执行时间与输入规模 $n$ 与 $n$ 的对数的乘积成正比。一些排序算法(如快速排序、归并排序等)的时间复杂度就是 $O(n \log n)$。
整体来讲 $O(n \log n)$ 的时间复杂度比 $O(n^2)$ 的时间复杂度要好,但是比 $O(n)$ 的时间复杂度要差。
计算斐波那契数列的时间复杂度也是 $O(n \log n)$。复习一下,一个斐波那契数列的开头是:$0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …$,其整体定义如下:
$$
f(n) = \begin{cases}
0, & \text{if } n = 0 \newline
1, & \text{if } n = 1 \newline
f(n-1) + f(n-2), & \text{if } n > 1
\end{cases}
\text{where } n \in \mathbb{N}_0
$$
也就是说,在这个数列中,第一项是 0,第二项是 1,之后的每一项都是前两项的和。
下面是 Java 中的代码实现:
1 | /** |
你将会发现,如果输入参数 $n$ 增加,由于递归的使用,其时间复杂度将以超过 $O(n)$ 的速度增长,但是不会超过 $O(n^2)$。
总结
大 $O$ 表示法是一种用于描述算法的效率的标准符号,它描述的是算法的时间复杂度,即算法执行所需的时间,以及这个时间如何随着输入规模的增加而变化。大部分情况下,我们关注的是算法时间复杂度函数的上界,即最坏情况下的时间复杂度。
要确定一个算法的时间复杂度,你基本只需要计算循环内部的代码执行了多少次,然后根据执行次数来确定时间复杂度。
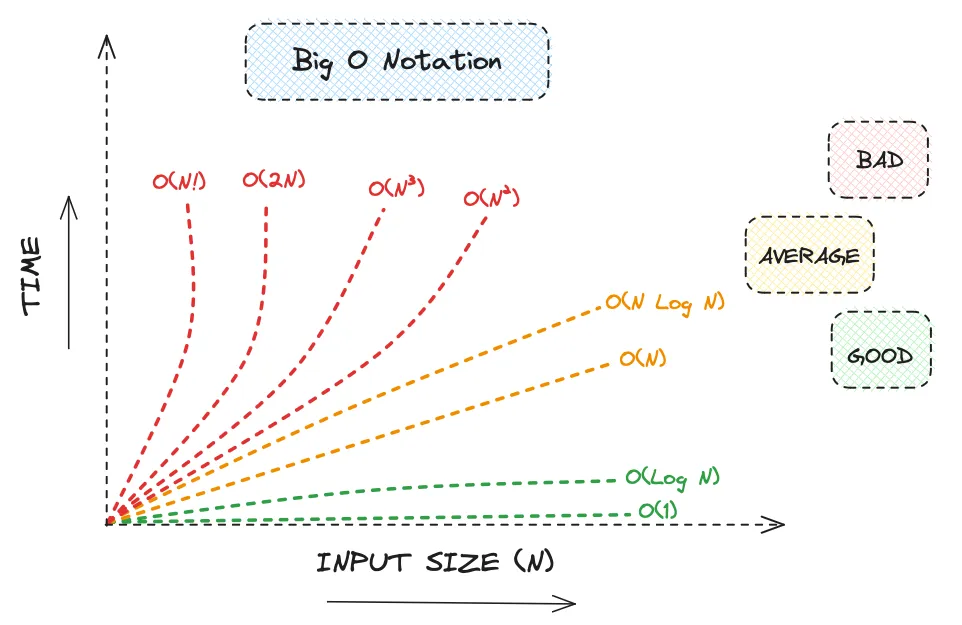
接下来是一个常见的时间复杂度的可视化图表:
GL & HF!